Batch 2 - Class 308 - Topology - Three utilities and inverting pant
zoom: send meeting Id and password
Start recording
Preclass Exercise:
- Explore the Klein bottle and projective plane puzzles on https://chalkdustmagazine.com/features/topological-tic-tac-toe/
Attendance: Anika, Vansh, Rhea Chadha, Ryan Chadha, Adyant, Aarushi, Ekagra, Ayush, Dhriti, Advay, Tarush, Kabir, Vivaan, Kushagra, Nikhil, Raghav, Shikhar, Yatharth, Aneesh, Mihir
Class Notes:
Revision
- Cutting Cylinders and Mobius strips
- Tic-Tac-Toe
- Mathematical model of cylinder, mobius strip, torus etc.
Homes and Utilities (Planar Graphs)
There are three homes and three utilities that must be supplied to each of the three homes, as under:
.png)
Can you connect each of the three utilities to each of the three houses, so that none of the pipelines cross?
Is there another way of placing the three houses and location of three utilities to make it happen? Can you prove that it can't be done?
If not, what is the least number of intersections you need to make it happen?
- Answer: You can do it with one intersection
.png)
If these were not on a flat surface, but on another kind of surface could you do it?
- Answer: Yes, it can be done on a torus
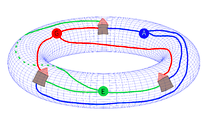
- Provide the following view for intuition, since this paper folds into a torus
.png)
Joining Segments
- MartinShCol 8.7 - See figure below and draw a line which intersects each of the 16 segments exactly once
- Answer: Can not be done because each of A, B, C have 5 sides each so a line can't enter and leave (even points of intersection) - note that two of these could be start and end points
- Can you do it on a Torus (Introduce the torus to kids)
- Yes, by having one point of entry "under" the drawing! (See bottom right solution)
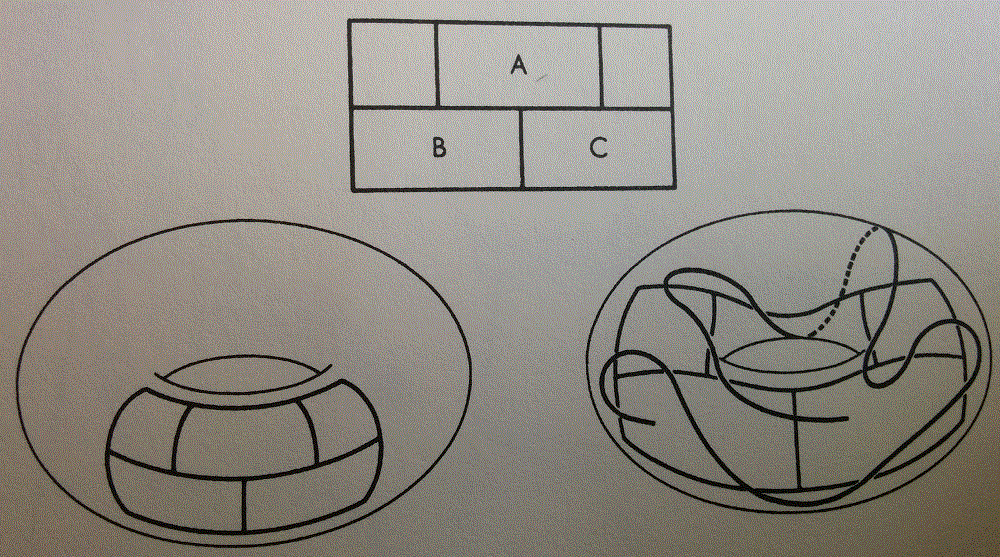
- In the problem above, can you attempt to find a surface where the loop can be closed?
Stretching and Bending
Topology is the study of shapes and surfaces. Any two objects that can be stretched or bent into each other (without tearing, punching holes or joining holes) are topologically similar.
- For example, a straw and donut are topologically the same, as is a coffee cup
- Can you stretch and bend the first donut into the second? How? (see https://www.youtube.com/watch?v=H8qwqGjOlSE around 2:45)
.png)
Homework Problem:
- If you had infinitely stretchy pants, could you turn them inside out without lifting your feet off the ground?
- Answer: https://www.youtube.com/watch?v=H8qwqGjOlSE (around 7:50)
References:
The Colossal Book of Short Puzzles and Problems, by Martin Gardner